在各位童鞋的期盼中，秋季的课程终于结束，迎来了我们欢喜的寒假时光，也意味着我们终于可以安心迎接新年的到来。

但作为新时代的好青年，未来的花朵，我们当然要看一看在过去的时间，我们学到了什么，有了怎样的成长。回顾整个的秋季学习时光，我们在高中数学这一科目中，知道了什么是集合；了解了函数的定义；扩充了我们对函数的认识，知道了除了一次函数、二次函数以外还有对数函数、指数函数；突然发现初中学习的正弦、余弦到高中居然变成了三角函数。仔细想想，在这一学期中，我们收获颇丰啊。

回顾了过去，我们同样还得看一看以后，看看在寒假我们又可以学到哪些东西呢！

首先整个寒假需要大家学习了解的数学知识有两部分：一、解三角形；二：空间几何体；

在初中时，我们对三角形的认知主要在一些特殊的三角形中，如等腰三角形、等边三角、直角三角形。对于这些三角形的边边角角，我们在求解时可以说是信手拈来。不过对于这些边边角角，我们高中也是需要求解的，只不过是由一些特殊的三角形变成了所有三角形；虽然问题变得复杂啦，但是我们同时也会有对应的工具来解决它，那就是我们在寒假需要学习的：正弦定理和余弦定理

定理的内容如下：在中，三个内角分别为A,B,C，其对边分别为a,b,c。

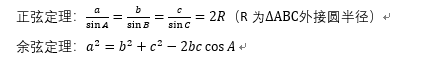
（余弦定理公式中的一个，其余两个，童鞋们可以自己尝试着写一下）

那么这两个定理都能解决什么问题呢？因为用途比较多，所以在这只和大家说一下定理的一个基础应用：

1.已知三角形的两角一边，求其余边角

2.已知三角形的两边及一边对角，求解其余边角

3.已知三角形的两边及夹角，求其余边角

4.求解三角形面积（无需求三角形的高哦！）

上面是寒假需要学习的第一个知识解三角形，接下来再说说另一个知识---空间几何体，

在初中时我们接触过平面几何的一些知识，如平面图形的面积；平面几何的证明。但这些都是一些二维空间的几何知识，但作为高中生的我们，岂是这些平面几何就能满足的，所以在寒假我们会学习一些三维空间的几何知识，但为了体现是由浅入深，我们先说一下简单的知识。

一、空间结合体的结构特征

听起来是不是及其具有逼格，但实际就是这样的，在这里你将知道原来我认识的几何体，它的概念怎么会和我想的不一样呢；求个面积、体积怎么会这么难呢。

空间几何体分为多面体、旋转体两类；多面体包含：棱柱、棱锥、棱台；旋转体包含：圆柱、圆锥、圆台、球体；

主要涉及的知识：各种几何体的概念、体积公式、面积公式等。

等学过这些，你会发现当你在看见水立方时，脑子里想的不再是：哇，好美；而是：我去，好标准的一个棱柱啊！

二、点线面的位置关系

我们之前接触的点线面的位置关系都是在二维空间中，那是如果有人问你，当两条直线没有交点时，它们的位置关系是什么？你会回答平行关系；但作为新时代的好青年，我们的回答怎能如此平庸呢！我们应该回答“它们的关系时平行或异面”

是的，此时我们接触的是三维空间，所以我们在研究点线面的位置关系时，不再是局限在一个平面中了，而是在广阔的三维空间。

此时线与线的关系会分为：共面关系、异面关系；线面关系：平行、相交以及直线在平面内；当然还有面与面的关系：平行、相交。

在学会了这些之后，我们就会开启立体几何的证明之路，证明：线线平行、线面平行、面面平行等，同时也会知道如何计算不在同一平面的直线所成的空间角，直线与平面形成的空间角等。

以上是寒假同学们需要在欢度假期时应该学习的数学知识，不然在假期后如何开启愉快的春季学习时光！